Cumulative Area To Z Score

A standard normal table (too chosen the unit normal table or z-score table) is a mathematical tabular array for the values of ϕ, indicating the values of the cumulative distribution part of the normal distribution. Z-Score, also known as the standard score, indicates how many standard deviations an entity is, from the mean.

Since probability tables cannot be printed for every normal distribution, equally in that location is an space variety of normal distribution, it is common practice to catechumen a normal to a standard normal and and then use the z-score tabular array to find probabilities.

Z-Score Formula

It is a style to compare the results from a test to a "normal" population.

If X is a random variable from a normal distribution with mean (μ) and standard deviation (σ), its Z-score may be calculated past subtracting mean from X and dividing the whole by standard deviation.

Z-Score Formula

Where, ten = test value

μ is mean and

σ is SD (Standard Deviation)

For the average of a sample from a population 'n', the hateful is μ and the standard difference is σ.

How to Interpret z-Score

Here is how to translate z-scores:

A z-score of less than 0 represents an chemical element less than the mean.
A z-score greater than 0 represents an chemical element greater than the mean.
A z-score equal to 0 represents an element equal to the mean.
A z-score equal to 1 represents an element, which is ane standard deviation greater than the mean; a z-score equal to 2 signifies 2 standard deviations greater than the hateful; etc.
A z-score equal to -i represents an chemical element, which is 1 standard divergence less than the mean; a z-score equal to -2 signifies 2 standard deviations less than the hateful; etc.
If the number of elements in the set is large, about 68% of the elements have a z-score between -1 and 1; about 95% accept a z-score betwixt -2 and 2 and about 99% have a z-score between -3 and 3.

z score graph

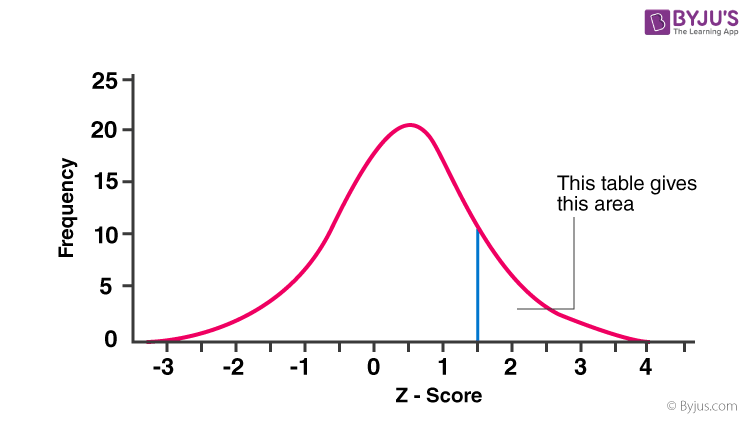
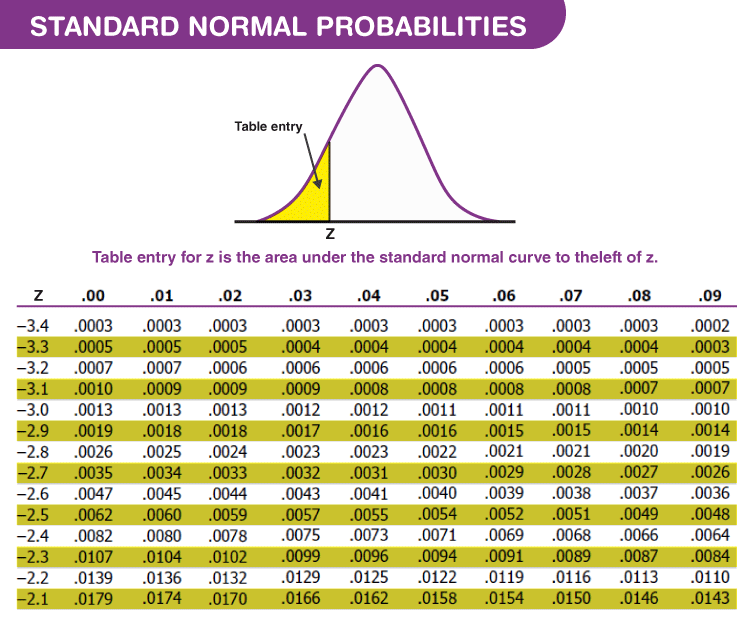
Z-Score table - 1
Z-Score table - 2

Z-Score table

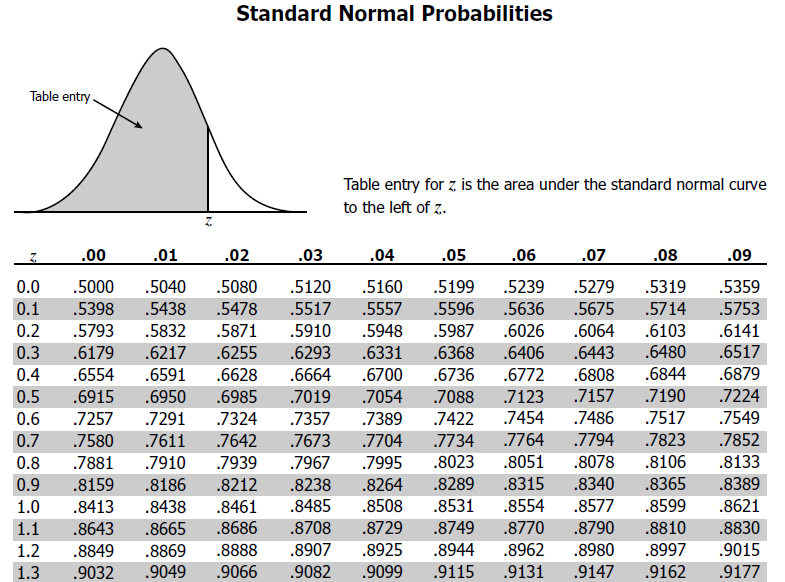
Example of Z Score

Let usa sympathise the concept with the help of a solved case:

Case: The test scores of students in a class test has a mean of 70 and with a standard divergence of 12. What is the probable percentage of students scored more than 85?

Solution: The z score for the given data is,

z= (85-seventy)/12=1.25

From the z score table, the fraction of the data within this score is 0.8944.

This means 89.44 % of the students are within the examination scores of 85 and hence the percentage of students who are to a higher place the test scores of 85 = (100-89.44)% = ten.56 %.

Frequently Asked Questions

What does the Z-Score Tabular array Imply?

The z score table helps to know the percentage of values below (to the left) a z-score in a standard normal distribution.

What are the Types of Z Score Table?

There are 2 z-score tables which are:

Positive Z Score Table: It means that the observed value is above the mean of total values.
Negative Z Score Tabular array: It means that the observed value is below the mean of total values.

What is Z Score and How is it calculated?

A z score is but defined every bit the number of standard departure from the mean. The z-score can be calculated by subtracting mean by test value and dividing it by standard value.

So, z = (10 − μ)/ σ

Where x is the test value, μ is the hateful and σ is the standard value.